EŞİTSİZLİKLER :: MATEMATİK

Anasayfa > EŞİTSİZLİKLER

A. BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ EŞİTSİZLİKLER

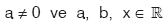olmak üzere,

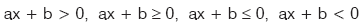
şeklindeki ifadelere birinci dereceden bir bilinmeyenli eşitsizlik adı verilir. Eşitsizliği çözmek için f(x) = ax + b fonksiyonunun tablosu yapılır. Eşitsizliği sağlayan aralık bulunur.

f(x) = ax + b fonksiyonunun işaret tablosu aşağıda verilmiştir.

ax + b = 0 denkleminin kökü 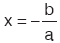dır.

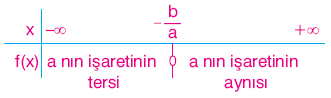
B. KISA YOLDAN FONKSİYONUN İŞARETİNİN İNCELENMESİ

Kısalığından dolayı bütün eşitsizliklerin çözüm yolunu kolayca bulabileceğiniz bir yaklaşım vereceğiz.

f(x), çarpım veya bölüm fonksiyonu olsun.

Tablo oluştururken sırasıyla şu işlemler yapılır:

1) f(x) in payı ile paydasını sıfır yapan değerler bulunup sırasıyla tabloya yazılır.

2) (Eşitsizliğin tanımı gözönüne alınarak) pay ile paydayı sıfır yapan değerlerden tek sayıda olanlarına tek katlı kök, çift sayıda olanlarına çift katlı kök denir.

3) Her bileşenin en büyük dereceli terimlerinin işaretleri çarpılarak veya bölünerek f(x) in işareti bulunur.

4) Tablodaki en büyük kökün sağındaki kutuya f(x) in işareti yazılır.

5) Tek katlı köklerin soluna sağındaki işaretinin tersi, çift katlı köklerin soluna sağındaki işaretin aynısı yazılır.

Kural

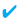ax² + bx + c > 0 eşitsizliğinin çözüm kümesi,

ise, (a > 0 ve D = b² - 4ac < 0) dır.

ax² + bx + c < 0 eşitsizliğinin çözüm kümesi, ise, (a < 0 ve D = b² - 4ac < 0) dır.

Uyarı

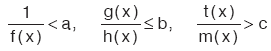gibi eşitsizliklerin çözüm kümesi bulunurken, içler dışlar çarpımı yapılamaz. Çünkü paydadaki f(x), h(x) ve m(x) in pozitif ya da negatif olduğunu bilmiyoruz.

Uyarı

gibi eşitsizliklerin çözüm kümesi bulunurken, g(x) = 0 ın kökleri kesri tanımsız yapacağından çözüm kümesine dahil edilmez.

C. İKİNCİ DERECEDEN DENKLEMLERİN KÖKLERİNİN İŞARETLERİNİN İNCELENMESİ

ax² + bx +c = 0 denkleminin köklerinin varlığını D, köklerinin işaretini 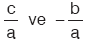belirler.

a × c < 0 ise denklemin farklı iki reel kökü vardır.

a × c > 0 ise denklemin denklemin köklerinin varlığı ile ilgili kesin bir şey söylenemez.

ax² + bx + c = 0 denkleminin kökleri x₁ ve x₂ olsun.

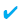Zıt işaretli köklerin olması için, 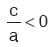olmalıdır.

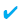(x₁ < 0 < x₂ ve 'x₁' > x₂) olması için, 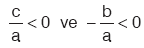olmalıdır.

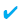(x₁ < 0 < x₂ ve 'x₁' < x₂) olması için, 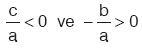olmalıdır.

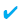Köklerin aynı işaretli olması için, 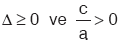olmalıdır.

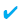0 < x₁ < x₂ olması için, 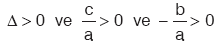olmalıdır.

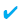x₁ < x₂ < 0 olması için, 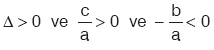olmalıdır

EŞİTSİZLİLER

Tablolar, sütun ve çizgi grafikleri, istatistiksel temsil biçimleridir. Grafik çizilirken eksenlerde yer alan sayılar arasında seçilen eşit birimdeki uzunluklara ölçek denir. Sütun grafikleri yatay ve dikey olarak çizilir. Sütun grafiğindeki çubuklar prizma şeklinde de çizilebilir. Grafik ve tablolar gerektiğinde numaralandırılır.

ÖRNEK
Aşağıdaki tabloda bir haftalık cep telefonu satışları verilmiştir.

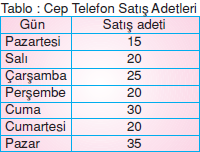
a) Tabloya ait, sütun ve çizgi grafiklerini çizelim.
b) 20 adet cep telefonu satıldığı günler hangileridir?
c) Satışlardaki en büyük artış hangi iki gün arasındadır?

ÇÖZÜM

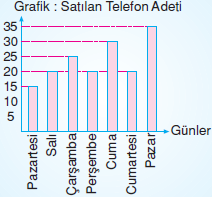
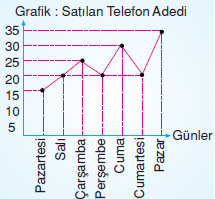
b) 20 adet cep telefonun satıldığı günler salı, perşembe ve cumartesidir.
c) Satışlardaki en büyük artış cumartesi ile pazar günleri arasındadır.

MERKEZİ EGİLİM VE YAYILMA ÖLÇÜLERİ

Aritmetik Ortalama

Verilerin toplamının veri sayısına bölümü verilerin aritmetik ortalamasını verir.

Örnek Soru

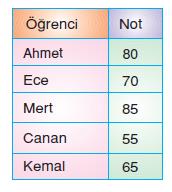
Yukarıdaki tabloda öğrenciler ve aldıkları notlar veriliyor.
Buna göre, öğrencilerin notlarının aritmetik ortalaması kaçtır?
A) 68 B) 69 C) 70 D)71

Çözüm

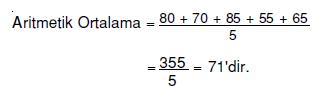
Yanıt D

Örnek Soru

Ali ve Cem'in yaşları toplamı 20'dir. Ali, Cem ve Deniz'in yaşları ortalaması 15'tir. Buna göre, Deniz kaç yaşındadır?
A) 25 B) 24 C) 23 D) 22

Ali, Cem ve Deniz'in yaşları toplamı 3.15 = 45'dir.
Ali ve Cem'in yaşları toplamı 20 olduğundan
Deniz'in yaşı 45 - 20 = 25 olur.
Yanıt A

Örnek Soru

12, 15, 20, 28, 30, 35, x
sayılarının aritmetik ortalamasının 25 olması için x kaç olmalıdır?
A) 42 B) 40 C) 38 D) 35

Çözüm

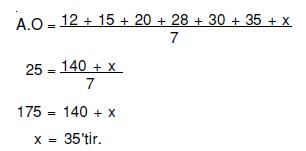
Yanıt D

Ortanca (Medyan)

Bir veri grubunda veriler küçükten büyüğe doğru sıralandığında ortada kalan veri ortanca değerdir.
Veri sayısı çift ise medyan ortada kalan iki sayının aritmetik ortalamasına eşittir.

Örnek Soru

10, 10, 12, 13, 10, 11, 8, 15, 16
Yukarıda 9 öğrencinin bir günde kaç sayfa kitap okudukları veriliyor.
Buna göre, okunan kitap sayfa sayılarının ortanca değeri kaçtır?
A) 10 B) 11 C)12 D)13

Çözüm

Sayfa sayılarını küçükten büyüğe doğru sıralayalım.

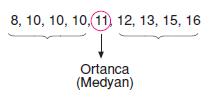
Yanıt B

Örnek Soru

12, 18, 24, 10, 15, 19
veri grubunun medyanı (ortanca) kaçtır?
A) 15 B) 16,5 C) 17,5 D) 18

Çözüm

Veri grubunu küçükten büyüğe doğru sıralayalım.

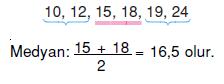
Yanıt B

Tepe Değeri (Mod)

Bir veri grubunda en fazla tekrar eden değer o veri grubunun tepe değeridir.

Örnek Soru

8, 9, 10, 10, 11, 8, 7, 7, 12, 10
veri grubunun tepe değeri kaçtır?
A)7 B)8 C)9 D)10

Çözüm

Verilen veri grubunda 2 tane 7, 2 tane 8, 1 tane 9, 3 tane 10, 1 tane 11 ve 1 tane 12 vardır.
En fazla tekrar eden 10 sayısı tepe değerdir.
Yanıt D

Örnek Soru

veri grubunun aritmetik ortalaması 33 olduğuna göre, modu ve medyanının toplamı kaçtır?
A) 73 B) 75 C) 77 D)80

Çözüm

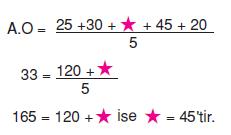
20, 25, 30, 45, 45 veri grubunun modu 45, medyanı 30'dur. Veri grubunun modu ve medyanının toplamı 45 + 30 = 75 olur.
Yanıt B

Örnek Soru

21, 18, 20, 32, 43, 21, 19, 26 veri grubu veriliyor.

Çözüm

Yanıt C

Örnek Soru

33, 47, 39, 42, 51, 39, 73, 55, 60

Yukarıdaki sayı dizisinin modu ile medyanın toplamı kaçtır?
A) 80 B) 82 C) 84 D) 86

Çözüm

33, 39, 39, 42, 47, 51, 55, 60, 73 sayı dizisinin modu 39, medyanı 47'dir. Dizinin modu ile medyanının toplamı 39 + 47 = 86 olur.
Yanıt D

NOT:Aritmetik ortalama, ortanca ve tepe değer merkezi eğilim ölçüleridir.

Merkezi Eğilim ve Yayılma Ölçüleri Etkin Katılım

20, 27, 24, 20, 18, 17, 16, 16, 30, 35, 32, 36, 36, 20, 20, 33
Yukarıda bir yarışmada yarışmacıların aldıkları puanlar verilmiştir.
Buna göre, aşağıdaki soruları cevaplayınız.

1. Kaç yarışmacı vardır?

2. Puanların aritmetik ortalaması kaçtır?

3. Kaç kişi aritmetik ortalamanın altında puan almıştır?

4. Puanların tepe değeri kaçtır?

5. Puanların ortancası kaçtır?